回転行列
「平面内の原点周りの回転操作」を考えます。この操作は実は線型性を持ちます。図形的に導きましょう。(動画参照)
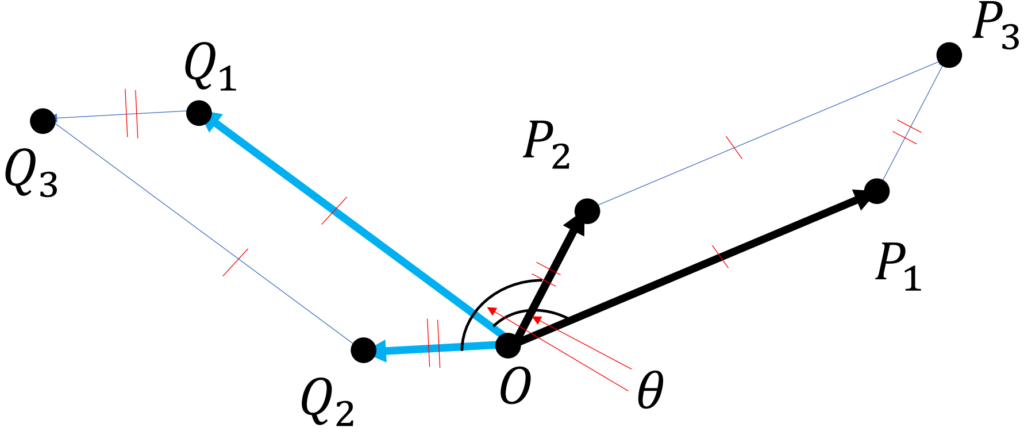
点\(P_1,P_2\)を任意にとり、四角形\(OP_1P_3P_2\)が平行四辺形になるように点\(P_3\)をとる。\(P_1,P_2,P_3\)を\(\theta\)回転させた点を\(Q_1,Q_2,Q_3\)とすると、回転は長さを変えないので四角形\(OQ_1Q_3Q_2\)は平行四辺形になる。よって、$$
\overrightarrow{OQ_{3}}=\overrightarrow{OQ_{1}}+\overrightarrow{OQ_{2}}$$
が成り立ち、これは回転操作が和をとる操作と交換可能であることを示している。
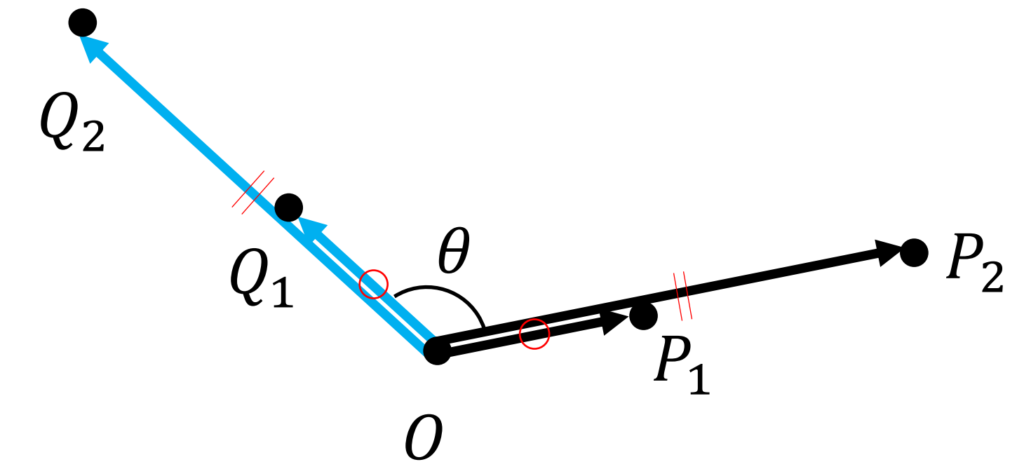
点\(P_1\)を任意にとり、直線\(OP_1\)上に点\(P_2\)をとる。\(\overrightarrow{OP_2}=k\overrightarrow{OP_1}\)(\(k\)は実数)と表せる。\(P_1,P_2\)を\(\theta\)回転させた点を\(Q_1,Q_2\)とすると、$$\overrightarrow{OQ_2}=k\overrightarrow{OQ_1}$$が成り立ち、これは回転操作がスカラー倍と交換可能であることを示している。
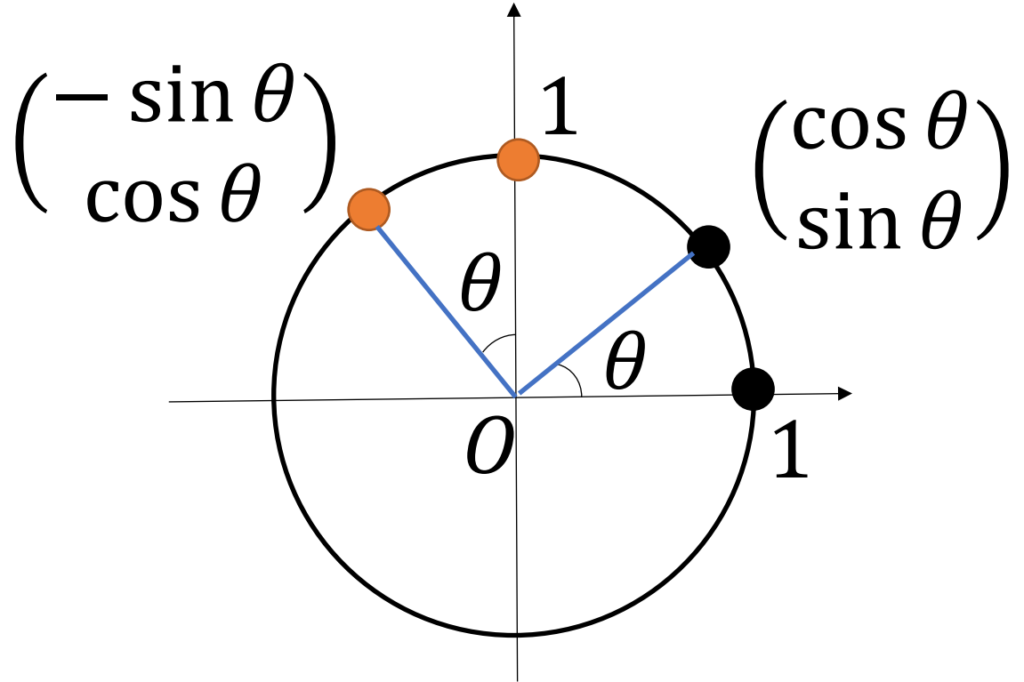
以上で回転操作の線型性は示せました。次に\(\theta\)回転に対応する行列を求めるため、\(\begin{pmatrix}1 \\ 0 \end{pmatrix},\begin{pmatrix}0 \\ 1 \end{pmatrix}\)の行先を求めます。それぞれ\(\begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix},\begin{pmatrix}-\sin \theta \\ \cos \theta \end{pmatrix}\)に移るのが上図から分かるので、対応する行列が求められました。
平面内で原点周りに\(\theta\)回転する操作は線型性をもつ。したがって対応する行列が存在する。その行列は、
$$
\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}
$$
$$
\begin{pmatrix} \dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} \\ \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{pmatrix}
(\theta =\frac{\pi}{4})$$$$
\begin{pmatrix} \dfrac{1}{2} & -\dfrac{\sqrt{3}}{2} \\ \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} \end{pmatrix}
(\theta =\frac{\pi}{3})
$$
点\(\begin{pmatrix}3 \\ 4\end{pmatrix}\)を\(\theta=\dfrac{\pi}{4}\)回転させた場合、どの点に移るか答えよ。
答.\(\begin{pmatrix}-\frac{1}{\sqrt{2}} \\ \frac{7}{\sqrt{2}}\end{pmatrix}\)(下記の計算を行って得た)$$
\begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}
\begin{pmatrix}3 \\ 4\end{pmatrix}=\begin{pmatrix}-\frac{1}{\sqrt{2}} \\ \frac{7}{\sqrt{2}}\end{pmatrix}$$
行列の積と線型関数の合成が対応していることを用いて、三角関数の加法定理を示せ。
答.\(\theta\)回転を表す関数を\(\varphi_\theta\) とおけば、$$
\varphi_{\alpha+\beta} = \varphi_\alpha \circ \varphi_\beta
$$\(\varphi_\theta\)は線型関数だから対応する行列がある。それを\(A_\theta\)とおけば、線型関数の合成と行列の積は対応しているから、$$
A_{\alpha+\beta}=A_{\alpha}A_{\beta}
$$
よって、$$
\begin{aligned}
\begin{pmatrix} \cos (\alpha+\beta) & -\sin (\alpha+\beta) \\ \sin (\alpha+\beta) & \cos (\alpha+\beta) \end{pmatrix}
&=\begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix}\begin{pmatrix} \cos \beta & -\sin \beta \\ \sin \beta & \cos \beta \end{pmatrix}\\
&=\begin{pmatrix} (\cos \alpha \cos \beta -\sin \alpha \sin \beta) & -(\sin \alpha \cos \beta +\cos \alpha \sin \beta) \\ (\sin \alpha \cos \beta +\cos \alpha \sin \beta) & (\cos \alpha \cos \beta -\sin \alpha \sin \beta) \end{pmatrix}
\end{aligned}$$
ゆえに両辺の(1,1)成分、(2,1)成分の等式から加法定理$$
\begin{aligned}
\cos (\alpha+\beta) &= \cos \alpha \cos \beta -\sin \alpha \sin \beta \\
\sin (\alpha+\beta) &=\sin \alpha \cos \beta +\cos \alpha \sin \beta
\end{aligned}
$$が得られた。
折り返し行列
「原点を通る直線に関する折り返し」を考えます。
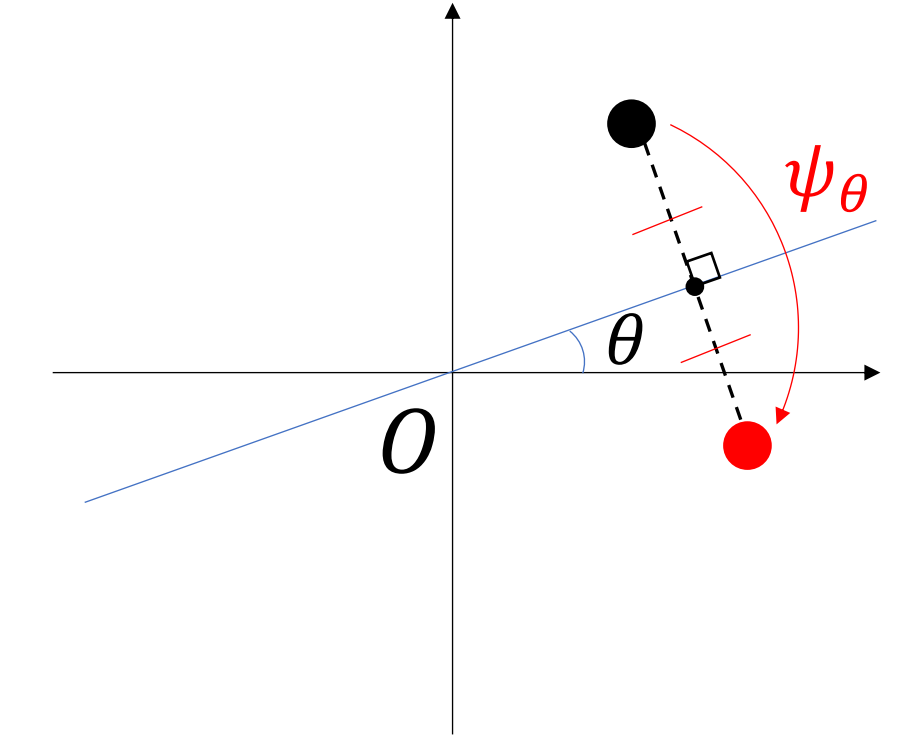
\(\theta\)回転を表す関数を\(\varphi_\theta\) , 原点を通る偏角\(\theta\)の直線に関する折り返しを表す関数を\(\psi_\theta\)とおきます。実は、
$$\psi_\theta=\varphi_\theta \circ \psi_0 \circ \varphi_{-\theta}
$$が成り立ちます。直線を\(x\)軸に重ねて(\(\varphi_{-\theta}\))、\(x\)軸に関して折り返して(\(\psi_0\))、直線をもとの位置に戻せば(\(\varphi_\theta\))、原点を通る偏角\(\theta\)の直線に関する折り返し(\(\psi_\theta\))になるからです(動画参照)。よって\(\psi_0\)についてのみ考えればよいです。\(\psi_0\)は\(x\)軸に関する折り返しですから、
$$\psi_0\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} x \\ -y \end{pmatrix}
$$が成り立ちます。各成分が\(x,y\)の一次の式になっていますので\(\psi_0\)は線型関数だと分かります。さらに、\(\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} x \\ -y \end{pmatrix}\)より、対応する行列は\(\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\)だということも分かります。また、\(\varphi_\theta\)は線型関数だったので、これらの合成として表せる\(\psi_\theta\)も線型関数だということになります。したがって、\(\psi_\theta\)に対応する行列\(B_\theta\)が存在します。
ここで、\(\varphi_\theta\)に対応する行列を\(A_\theta\)とおき、線型関数の合成と行列の積が対応していること用いれば、$$
\begin{aligned}B_\theta &=A_\theta B_0 A_{-\theta} \\
&=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \\
&=\begin{pmatrix} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{pmatrix}
\end{aligned}
$$
平面内で原点を通る偏角\(\theta\)の直線に関する折り返しは線型性をもつ。したがって対応する行列が存在する。その行列は、$$
\begin{pmatrix} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{pmatrix}
$$または、三角関数の加法定理によって、$$
\begin{pmatrix} \dfrac{1-\tan^2\theta}{1+\tan^2\theta} & \dfrac{2\tan\theta}{1+\tan^2\theta} \\
\dfrac{2\tan\theta}{1+\tan^2\theta} & -\dfrac{1-\tan^2\theta}{1+\tan^2\theta} \end{pmatrix}
$$
$$
\begin{aligned}
\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}(\theta=0)&(x軸に関する折り返し) \\
\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}(\theta=\dfrac{\pi}{4})&(直線y=xに関する折り返し)\\
\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}(\theta=\dfrac{\pi}{2})&(y軸に関する折り返し)
\end{aligned}$$
点\(\begin{pmatrix}3 \\ 4\end{pmatrix}\)を直線\(y=x\)で折り返した場合、どの点に移るか答えよ。
答.\(\begin{pmatrix}4 \\ 3 \end{pmatrix}\)(下記の計算を行って得た)$$
\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
\begin{pmatrix}3 \\ 4\end{pmatrix}=\begin{pmatrix}4 \\ 3\end{pmatrix}$$
点\(\begin{pmatrix}3 \\ 4\end{pmatrix}\)を直線\(y=mx\)で折り返した場合、どの点に移るか答えよ。
答.\(\begin{pmatrix} \dfrac{3-8m-3m^2}{1+m^2} \\ \dfrac{-4+6m+4m^2}{1+m^2} \end{pmatrix}\)(下記の計算を行って得た)
直線の偏角を\(\theta\)とおけば、\(m=\tan\theta\)と表せるので、$$
\begin{aligned}
\begin{pmatrix} \dfrac{1-\tan^2\theta}{1+\tan^2\theta} & \dfrac{2\tan\theta}{1+\tan^2\theta} \\
\dfrac{2\tan\theta}{1+\tan^2\theta} & -\dfrac{1-\tan^2\theta}{1+\tan^2\theta} \end{pmatrix}
\begin{pmatrix}3 \\ 4\end{pmatrix}
&=\begin{pmatrix} \dfrac{1-m^2}{1+m^2} & \dfrac{2m}{1+m^2} \\
\dfrac{2m}{1+m^2} & -\dfrac{1-m^2}{1+m^2} \end{pmatrix}\begin{pmatrix}3 \\ 4\end{pmatrix}\\
&=\begin{pmatrix} \dfrac{3-8m-3m^2}{1+m^2} \\ \dfrac{-4+6m+4m^2}{1+m^2} \end{pmatrix}
\end{aligned}
$$
