解の存在
解が存在しない例
連立一次方程式は場合によっては解が存在しません。
$$
\begin{cases}
x_1&=&1\\
x_1&=&2
\end{cases}
$$この連立一次方程式は解が存在しない。\(1\neq 2\) だからである。
解が存在しないのは、このような明らかな場合だけではありません。次の例のように、ぱっと見て解が存在しないと断言できないものもあります。
$$
\begin{cases}
x_1&+2x_2&=&1\\
-2x_1&-4x_2&=&2
\end{cases}
$$この連立一次方程式は解が存在しない。掃き出し法で変形すると、$$
\left(\begin{array}{cc|c}
1&2&1\\
-2&-4&1
\end{array}\right)
\rightarrow
\left(\begin{array}{cc|c}
1&2&1\\
0&0&3
\end{array}\right)
$$したがって、次のような連立一次方程式になるので、解が存在しないと断言できる。$$
\begin{cases}
x_1&+2x_2&=&1\\
&0&=&3
\end{cases}
$$
次の例も見てみましょう。
$$
\begin{aligned}
&\left(\begin{array}{ccc|c}
1&0&1&1\\
1&2&3&5\\
-2&2&0&3
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{ccc|c}
1&0&1&1\\
&2&2&4\\
&2&2&5
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{ccc|c}
1&0&1&1\\
&2&2&4\\
&&&1
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{ccc|c}
1&0&1&1\\
&1&1&2\\
&&&1
\end{array}\right)
\end{aligned}
$$よって第 \(3\) 行を見れば、解が存在しないことが分かる。
解が存在しない例に共通することは、拡大係数行列の変形途中において、
階段行列にしたとき、「\(0=(0\)でない数)」という等式が現れる。
ということです。解が存在する場合と比較していきましょう。
解が存在する例
上の具体例と非常に似た次の連立一次方程式を考えます。係数行列は全く同じものです。
$$
\begin{aligned}
&\left(\begin{array}{ccc|c}
1&0&1&1\\
1&2&3&5\\
-2&2&0&2
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{ccc|c}
1&0&1&1\\
&2&2&4\\
&2&2&4
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{ccc|c}
1&0&1&1\\
&2&2&4\\
&&&
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{ccc|c}
1&0&1&1\\
&1&1&2\\
&&&
\end{array}\right)
\end{aligned}
$$これは次の連立一次方程式を表す。$$
\begin{cases}
x_1&&+x_3&=&1\\
&x_2&+x_3&=&2
\end{cases}
$$よって、解は存在し、任意定数 \(t\) を用いて、次のように表せる。$$
\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}
=\begin{pmatrix}1\\2\\0\end{pmatrix}
+t\begin{pmatrix}-1\\-1\\1\end{pmatrix}
$$
よって、解が存在するための条件は次のように述べることができます。
連立一次方程式 \(A\vec x=\vec b\) において、$$
(A|\vec b) \rightarrow
\left(
\begin{array}{cccccccc|c}
1&*&*&*&*&*&*&*&*\\
0&0&1&*&*&*&*&*&*\\
0&0&0&0&0&1&*&*&*\\
0&0&0&0&0&0&0&0&d_1\\
0&0&0&0&0&0&0&0&d_2
\end{array}
\right)
$$のように掃き出し法で階段行列にしたとき、解が存在するための必要十分条件は、$$
d_1=d_2=0$$
つまり、階段行列の最終列では段差がないということが条件だということです。
$$
\begin{pmatrix}1&2\\2&4\end{pmatrix}
\begin{pmatrix}x_1\\x_2\end{pmatrix}
=\begin{pmatrix}2c\\c+1\end{pmatrix}
$$が解をもつとき、\(c\) の値を求め、そのときの解を求めよ。
(解答)$$
\begin{aligned}
&\left(\begin{array}{cc|c}
1&2&2c\\
2&4&c+1
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{cc|c}
1&2&2c\\
&&-3c+1
\end{array}\right)
\end{aligned}
$$解が存在するのは、\(-3c+1=0\) の場合に限るので、求める \(c\) の値は \(c=\frac{1}{3}.\)
\(c=\frac{1}{3}\) のとき、拡大係数行列は、$$
\left(\begin{array}{cc|c}
1&2&\frac{2}{3}\\
&&
\end{array}\right)
$$となるので、解は、任意定数を \(t\) として、$$
\begin{pmatrix}x_1\\x_2\end{pmatrix}
=\begin{pmatrix}\frac{2}{3}\\0\end{pmatrix}
+t\begin{pmatrix}-2\\1\end{pmatrix}.$$
連立一次方程式の解の存在条件は次のように述べることもできます。
連立一次方程式 \(A\vec x=\vec b\) において、解が存在するための必要十分条件は、$$
\text{rank}A=\text{rank}(A|\vec b)$$
基本変形しても行列の階数(rank)は変わらないので、拡大係数行列 \((A|\vec b)\) は階段行列になっているとして一般性を失わない。
解が存在すれば、最終列で段差ができないので、$$
\text{rank}A=\text{rank}(A|\vec b)$$
解が存在しなければ、最終列で段差ができるので、$$
\text{rank}(A|\vec b)=\text{rank}A+1$$ゆえに、$$
\text{rank}A\neq \text{rank}(A|\vec b)$$
解の構造
連立一次方程式は次の二つに分類されます。
- 斉次連立一次方程式:\(A\vec x=0\)
- 非斉次連立一次方程式:\(A\vec x=\vec b (\vec b \neq 0)\)
※斉次・・・等式の両辺の次数がそろっていることを意味する。各項が各変数に関して全て一次式なら斉次、\(0\) 次式(\(0\) でない定数項のこと)が現れていたら非斉次という。
斉次連立一次方程式
斉次形ならば、拡大係数行列は \((A|\vec 0)\) となるので、解が必ず存在します。
$$\left(
\begin{array}{cccc|c}
1&a_2&0&a_4&0\\
0&0&1&b_4&0\\
0&0&0&0&0
\end{array}
\right)$$この拡大係数行列が表すのは斉次形の連立一次方程式である。解は、\(2\) 個の任意定数 \(s,t\) を用いて、$$
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=s\begin{pmatrix}-a_2\\1\\0\\0\end{pmatrix}
+t\begin{pmatrix}-a_4\\0\\-b_4\\1\end{pmatrix}
$$となる。
前回、掃き出し法によって、様々な連立一次方程式の解を求めましたが、斉次形の場合は、上の例のように特徴的な形になっていたことが確認できると思います。この事実をまとめます。
- 斉次連立一次方程式は解を必ずもつ。
- 解の形はいくつかの任意定数 \(t_1,t_2,…,t_l\) と適当なベクトル \(\vec v_1,\vec v_2,…,\vec v_l\) を用いて$$
\vec x =t_1\vec v_1+t_2\vec v_2+\dots +t_l\vec v_l
$$と表すことができる。
※このような場合、解の自由度が \(l\) であるといったり、解の空間が \(l\) 次元であると言ったりする。次元については今後の記事で詳しく述べる。
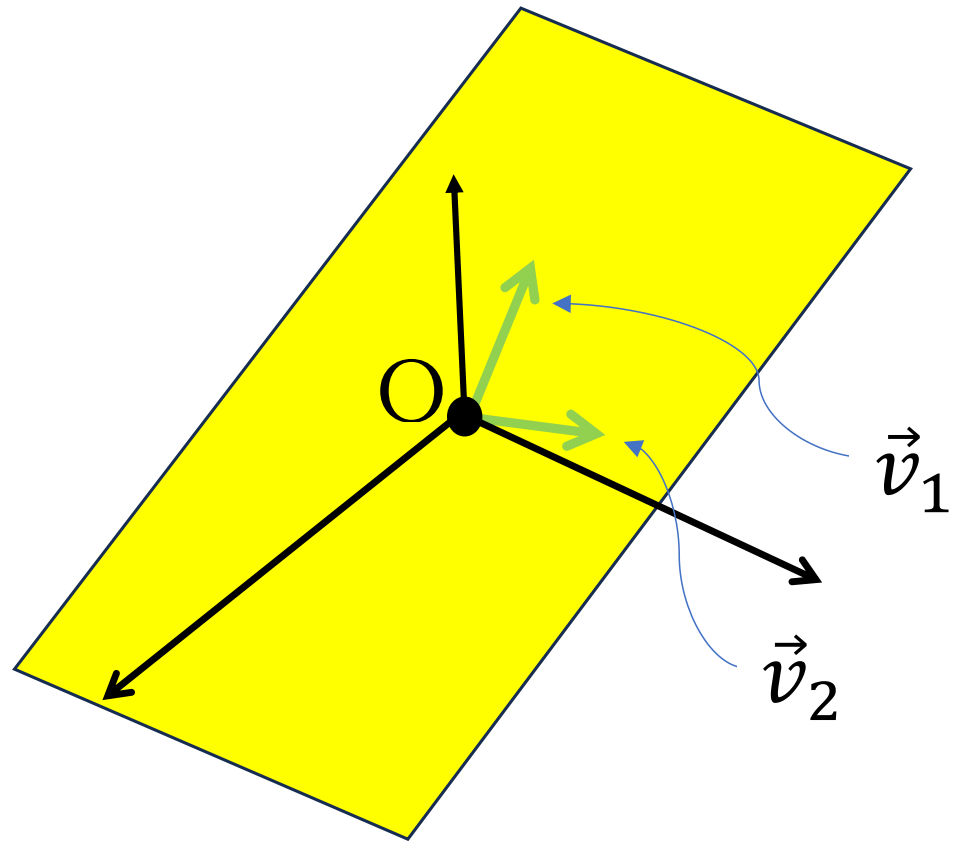
例えば自由度が \(2\) の場合は \(\vec x=t_1\vec v_1+t_2\vec v_2\) のように表せるので、解は左図のような原点を通る平面になります。
非斉次連立一次方程式
非斉次連立一次方程式の場合は解が存在しない場合もあります。存在する場合のみ考えます。
$$\left(
\begin{array}{cccc|c}
1&a_2&0&a_4&d_1\\
0&0&1&b_4&d_2\\
0&0&0&0&0
\end{array}
\right)$$この拡大係数行列が表すのは非斉次形の連立一次方程式である。解は、\(2\) 個の任意定数 \(s,t\) を用いて、$$
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=\begin{pmatrix}d_1\\0\\d_2\\0\end{pmatrix}
+s\begin{pmatrix}-a_2\\1\\0\\0\end{pmatrix}
+t\begin{pmatrix}-a_4\\0\\-b_4\\1\end{pmatrix}
$$となる。
- 非斉次連立一次方程式は解が存在しないことがある。
- 解は非斉次解の一つと斉次解の和になる。
したがって、解の形は、非斉次解の一つ \(\vec y\) と、いくつかの任意定数 \(t_1,t_2,…,t_l\) と適当なベクトル \(\vec v_1,\vec v_2,…,\vec v_l,\) を用いて$$\vec x =\vec y+t_1\vec v_1+t_2\vec v_2+\dots +t_l\vec v_l$$と表すことができる。
非斉次解 \(\vec y\) を一つ見つければ、他のどの非斉次解 \(\vec x\) も 「\(\vec x=\vec y +\) (斉次解)」 と表せるということです。
(証明)
任意の非斉次解を \(\vec x\) とおく。解が存在する場合を考えているので、その解の一つが得られたとして \(\vec y\) とする。\(\vec z =\vec x -\vec y\) とおき、\(\vec z\) について考える。$$
\begin{aligned}
A\vec z&=A(\vec x-\vec y)\\
&=A\vec x-A\vec y\\
&=\vec b-\vec b\\
&=0
\end{aligned}
$$よって、\(\vec z\) は斉次解である。\(\vec z =\vec x -\vec y\) より、\(\vec x =\vec y +\vec z.\) すなわち、任意の解は非斉次解の一つと斉次解の和になることが言えた。(証明終)
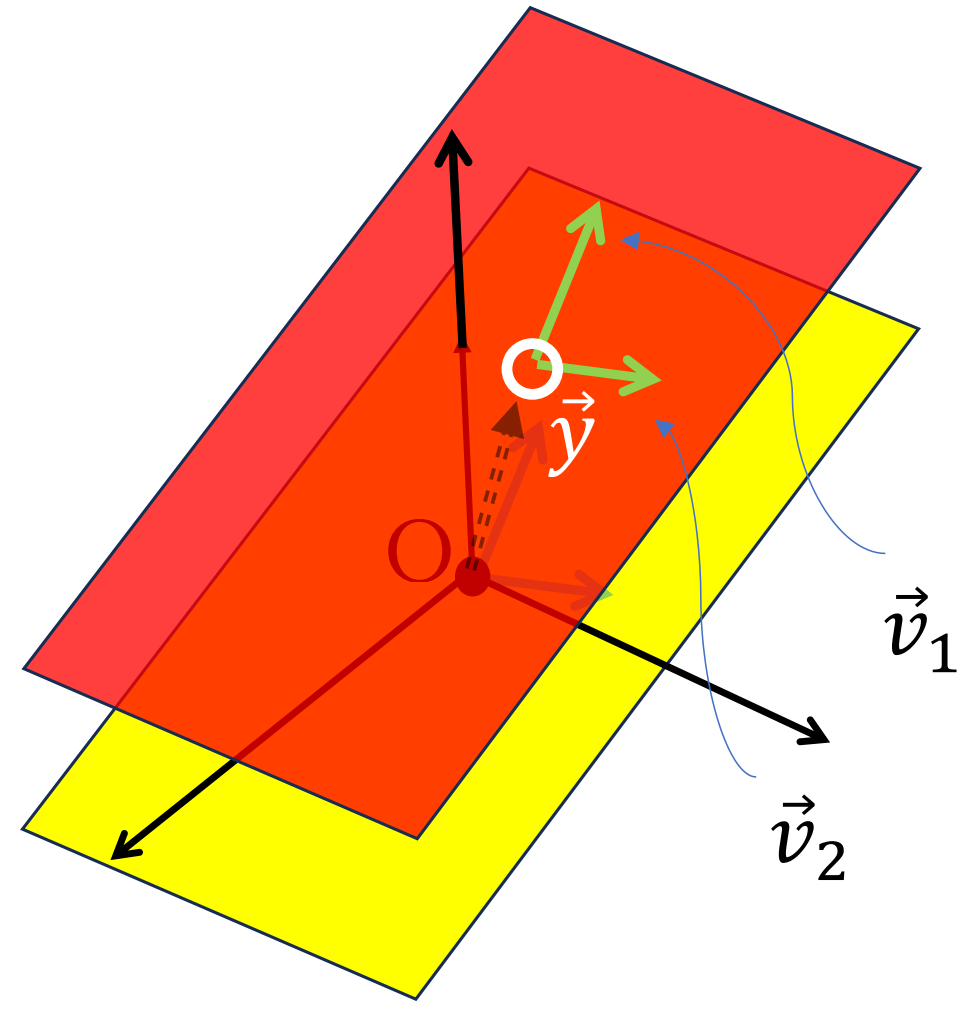
斉次方程式の解の自由度が \(2\) の場合は \(\vec x=\vec y+t_1\vec v_1+t_2\vec v_2\) のように表せるので、解は左図のような原点を通らない赤い平面になります。原点を通る黄色い平面は斉次解を表しています。斉次解を \(\vec y\) だけ平行移動させた図形が、非斉次解だということです。
係数行列の階数(rank)が担う重要な役割
非斉次解は斉次解でほぼ決まるので、斉次形の連立一次方程式を考えていきます。
階数(rank)は本質的に必要な方程式の個数である
係数行列の階数(rank)は非斉次方程式の解の存在条件を表現することができました。実は階数(rank)の役割はそれだけではありません。まず言えることは、「本質的に必要な方程式の個数」を表しているということです。
$$
\begin{cases}
x_1&&+x_3&+2x_4&=&0\\
x_1&+x_2&+4x_3&+6x_4&=&0\\
2x_1&+x_2&+5x_3&+8x_4&=&0
\end{cases}
$$掃き出し法で変形すると、$$
\begin{aligned}
&\left(\begin{array}{cccc|c}
1&0&1&2&0\\
1&1&4&6&0\\
2&1&5&8&0
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{cccc|c}
1&0&1&2&0\\
&1&3&4&0\\
&1&3&4&0
\end{array}\right)\\
\\
\rightarrow
&\left(\begin{array}{cccc|c}
1&0&1&2&0\\
&1&3&4&0\\
&&&&
\end{array}\right)
\end{aligned}$$したがって、方程式は次のように同値変形できる。$$
\begin{cases}
x_1&&+x_3&+2x_4&=&0\\
&+x_2&+3x_3&+4x_4&=&0
\end{cases}
$$ここまで、変形すれば、\(x_3,x_4\) に任意定数を代入すれば解を求めることができる。最初に \(3\) 個の方程式が与えられていたが、本質的に必要な方程式の個数は \(3\) 個ではなくて、\(2\) 個だったということになる。そして、係数行列の階数(rank)も \(2\) である。これらは一致している。
\(A\) を \((m,n)\) 型の行列とする。方程式 \(A\vec x=0\) は \(n\) 変数の \(m\) 個の連立一次方程式である。\(m\) 個の方程式の内、本質的に必要な方程式の個数は \(\text{rank}A\) の値と等しくなる。
階数(rank)と解の自由度の関係
階数(rank)の役割はまだあります。次に言えることは、「解の自由度」を求めることができるということです。
「(非斉次解)=(非斉次解のひとつ)+(斉次解)」が成り立つので、斉次解の自由度が非斉次解の形も決定することになります。解の自由度は係数行列の階数(rank)と密接な関係があります。
$$
\begin{pmatrix}
1&a&b&c\\
&&&\\
&&&
\end{pmatrix}
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=\vec 0
$$この方程式の解は、$$
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=t_1\begin{pmatrix}-a\\1\\0\\0\end{pmatrix}
+t_2\begin{pmatrix}-b\\0\\1\\0\end{pmatrix}
+t_3\begin{pmatrix}-c\\0\\0\\1\end{pmatrix}
$$係数行列の階数(rank): \(1\)
解の自由度: \(3\)
変数の個数: \(4\)
$$
\begin{pmatrix}
1&0&1&2\\
&1&3&4\\
&&&
\end{pmatrix}
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=\vec 0
$$この方程式の解は、$$
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=t_1\begin{pmatrix}-1\\-3\\1\\0\end{pmatrix}
+t_2\begin{pmatrix}-2\\-4\\0\\1\end{pmatrix}
$$係数行列の階数(rank): \(2\)
解の自由度: \(2\)
変数の個数: \(4\)
$$
\begin{pmatrix}
1&0&0&p\\
&1&0&q\\
&&1&r
\end{pmatrix}
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=\vec 0
$$この方程式の解は、$$
\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
=t\begin{pmatrix}-p\\-q\\-r\\1\end{pmatrix}
$$係数行列の階数(rank): \(3\)
解の自由度: \(1\)
変数の個数: \(4\)
これらの具体例を通して、(係数行列の階数(rank))+(解の自由度)=(変数の個数)が成り立っていることが分かるでしょう。
行列の階数(rank)は行基本変形で変わらないので、一般に次のことが言えます。
次の斉次連立一次方程式において、$$
\begin{pmatrix}
a_{11}&a_{12}&\dots&a_{1n}\\
a_{21}&a_{22}&\dots&a_{2n}\\
\vdots&\vdots&\vdots&\vdots\\
a_{m1}&a_{m2}&\dots&a_{mn}
\end{pmatrix}
\begin{pmatrix}
x_1\\x_2\\\vdots\\x_n
\end{pmatrix}
=\vec 0
$$
係数行列を \(A,\) (解の自由度) を \(s\) とおけば、次が成り立つ。$$
\text{rank}A+s=n
$$
非斉次方程式の任意定数の個数は、斉次方程式の解の自由度に他なりませんから、次の例も挙げられます。
$$\left(
\begin{array}{cccccccc|c}
1&*&*&*&*&*&*&*&*\\
0&0&1&*&*&*&*&*&*\\
0&0&0&0&0&1&*&*&*\\
0&0&0&0&0&0&0&0&0\\
0&0&0&0&0&0&0&0&0
\end{array}
\right)
$$「この拡大係数行列が表す連立一次方程式の解は、任意定数を \(5\) 個もつ。\(1\) が書いていない列、すなわち \(2,4,5,7,8\) に対応する \(x_2,x_4,x_5,x_7,x_8\) に任意定数を代入して解けばよい。」
と前回の記事で説明したが、この例の場合、係数行列の階数(rank)、任意定数の個数、変数の個数がそれぞれ \(3,5,8\) である。\(3+5=8\) だから確かに上で述べたことが成り立っている。
係数行列の正則性
ここまでの知識を踏まえて、行列の正則性の条件を得ることができます。
\(A\) を \(n\) 次正方行列とする。次の条件は同値である。
- \(A\) が正則である。
- 斉次一次方程式 \(A\vec x=\vec 0\) は自明な解しかもたない。
\(A\vec x=\vec 0\) における自明な解:\(\vec x=\vec 0\) のことである。
\(A\) が正則ならば、逆行列 \(A^{-1}\) を方程式 \(A\vec x=\vec 0\) の両辺にかければ、自明な解しか存在しないことがわかる。
逆に、方程式 \(A\vec x=\vec 0\) が自明な解しかもたないとする。\(s=\)(解の自由度) とおくと、\(s=0,\) \(\text{rank}A+s=n\) であるから、\(\text{rank}A=n\) が成り立つ。これは \(A\) が正則であることを意味するのであった。
ここまでで、行列の正則性に関する条件がいくつかでてきたので、以下にまとめておきます。
\(A\) を \(n\) 次正方行列とする。以下の条件は全て同値である。
- \(A\) が正則である。
- \(\text{rank}A=n.\)
- \(A\) は基本行列の有限個の積である。
- \(AB=E\) となる \(n\) 次正方行列 \(B\) が存在する。
- \(BA=E\) となる \(n\) 次正方行列 \(B\) が存在する。
- 斉次一次方程式 \(A\vec x=\vec 0\) は自明な解しかもたない。
今後、線型代数学で扱う重要なテーマは行列の固有値です。\(\alpha \) が正方行列 \(A\) の固有値であるとは、$$
A\vec x=\alpha \vec x
$$が自明でない解 \(\vec x\neq 0\) をもつことを表します。この \(\vec x\) を \(\alpha\) の固有ベクトルといいます。図形的には、固有ベクトルの方向に行列 \(A\) をかけることは、単に \(\alpha\) 倍しただけの動きになります。一般には行列をかけると変な方向に移動してしまいますが、固有ベクトルはそうではないのです。そして、固有ベクトル全て求めることで、行列の、ひいては線型変換の完全な理解を可能にします(場合によっては、広義固有ベクトルまで求める必要がある)。したがって、固有値は重要です。固有値を求めるためには、移項して整理した次の等式$$
(\alpha E -A)\vec x=\vec 0
$$が自明でない解をもつような \(\alpha\) を求めればよいです。このようにして、「斉次一次方程式が自明でない解をもつ場合」は今後も扱っていきます。上にまとめた条件から、\(\alpha E -A\) が正則でないような \(\alpha\) を求められればよいのですが、ここに述べた同値条件だと簡単に求められないことが多いです。そこで、行列式 \(\det\) が歓迎されます。実は \(\det A\neq 0\) は \(A\) が正則であることと同値なのです。固有値 \(\alpha\) を求めるためには係数行列が正則でないような場合を考えればよいので、 \(\det (\alpha E-A)=0\) を計算して確かめればよいです。それではどのようにして計算すればよいか、そもそも行列式 \(\det\) とは何なのか、次の記事から説明していきたいと思います。
